Group Lasso Regularization

This is an example demonstrating Pyglmnet with group lasso regularization, typical in regression problems where it is reasonable to impose penalties to model parameters in a group-wise fashion based on domain knowledge.

# Author: Matthew Antalek <matthew.antalek@northwestern.edu>
# License: MIT

from pyglmnet import GLMCV
from pyglmnet.datasets import fetch_group_lasso_datasets
import matplotlib.pyplot as plt

Group Lasso Example applied to the same dataset found in: ftp://ftp.stat.math.ethz.ch/Manuscripts/buhlmann/lukas-sara-peter.pdf

The task here is to determine which base pairs and positions within a 7-mer sequence are predictive of whether the sequence contains a splice site or not.

Read and preprocess data

df, group_idxs = fetch_group_lasso_datasets()
print(df.head())

Out:

...0%, 0 MB
...8%, 0 MB
...16%, 0 MB
...24%, 0 MB
...32%, 0 MB
...40%, 0 MB
...48%, 0 MB
...56%, 0 MB
...64%, 0 MB
...73%, 0 MB
...81%, 0 MB
...89%, 0 MB
...97%, 0 MB

...100%, 0 MB

...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...2%, 0 MB
...2%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...5%, 0 MB
...5%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...8%, 0 MB
...8%, 0 MB
...9%, 0 MB
...9%, 0 MB
...9%, 0 MB
...10%, 0 MB
...10%, 0 MB
...11%, 0 MB
...11%, 0 MB
...11%, 0 MB
...12%, 0 MB
...12%, 0 MB
...12%, 0 MB
...13%, 0 MB
...13%, 0 MB
...14%, 0 MB
...14%, 0 MB
...14%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...16%, 0 MB
...16%, 0 MB
...17%, 0 MB
...17%, 0 MB
...17%, 0 MB
...18%, 0 MB
...18%, 0 MB
...19%, 0 MB
...19%, 0 MB
...19%, 0 MB
...20%, 0 MB
...20%, 0 MB
...20%, 0 MB
...21%, 0 MB
...21%, 0 MB
...22%, 0 MB
...22%, 0 MB
...22%, 0 MB
...23%, 0 MB
...23%, 0 MB
...23%, 0 MB
...24%, 0 MB
...24%, 0 MB
...25%, 0 MB
...25%, 0 MB
...25%, 0 MB
...26%, 0 MB
...26%, 0 MB
...27%, 0 MB
...27%, 0 MB
...27%, 0 MB
...28%, 0 MB
...28%, 0 MB
...28%, 0 MB
...29%, 0 MB
...29%, 0 MB
...30%, 0 MB
...30%, 0 MB
...30%, 0 MB
...31%, 0 MB
...31%, 0 MB
...31%, 0 MB
...32%, 0 MB
...32%, 0 MB
...33%, 0 MB
...33%, 0 MB
...33%, 0 MB
...34%, 0 MB
...34%, 0 MB
...35%, 0 MB
...35%, 0 MB
...35%, 0 MB
...36%, 0 MB
...36%, 0 MB
...36%, 0 MB
...37%, 0 MB
...37%, 0 MB
...38%, 0 MB
...38%, 0 MB
...38%, 0 MB
...39%, 0 MB
...39%, 0 MB
...39%, 0 MB
...40%, 0 MB
...40%, 0 MB
...41%, 0 MB
...41%, 0 MB
...41%, 0 MB
...42%, 0 MB
...42%, 0 MB
...42%, 0 MB
...43%, 0 MB
...43%, 0 MB
...44%, 0 MB
...44%, 0 MB
...44%, 0 MB
...45%, 0 MB
...45%, 0 MB
...46%, 0 MB
...46%, 0 MB
...46%, 0 MB
...47%, 0 MB
...47%, 0 MB
...47%, 0 MB
...48%, 0 MB
...48%, 1 MB
...49%, 1 MB
...49%, 1 MB
...49%, 1 MB
...50%, 1 MB
...50%, 1 MB
...50%, 1 MB
...51%, 1 MB
...51%, 1 MB
...52%, 1 MB
...52%, 1 MB
...52%, 1 MB
...53%, 1 MB
...53%, 1 MB
...54%, 1 MB
...54%, 1 MB
...54%, 1 MB
...55%, 1 MB
...55%, 1 MB
...55%, 1 MB
...56%, 1 MB
...56%, 1 MB
...57%, 1 MB
...57%, 1 MB
...57%, 1 MB
...58%, 1 MB
...58%, 1 MB
...58%, 1 MB
...59%, 1 MB
...59%, 1 MB
...60%, 1 MB
...60%, 1 MB
...60%, 1 MB
...61%, 1 MB
...61%, 1 MB
...62%, 1 MB
...62%, 1 MB
...62%, 1 MB
...63%, 1 MB
...63%, 1 MB
...63%, 1 MB
...64%, 1 MB
...64%, 1 MB
...65%, 1 MB
...65%, 1 MB
...65%, 1 MB
...66%, 1 MB
...66%, 1 MB
...66%, 1 MB
...67%, 1 MB
...67%, 1 MB
...68%, 1 MB
...68%, 1 MB
...68%, 1 MB
...69%, 1 MB
...69%, 1 MB
...70%, 1 MB
...70%, 1 MB
...70%, 1 MB
...71%, 1 MB
...71%, 1 MB
...71%, 1 MB
...72%, 1 MB
...72%, 1 MB
...73%, 1 MB
...73%, 1 MB
...73%, 1 MB
...74%, 1 MB
...74%, 1 MB
...74%, 1 MB
...75%, 1 MB
...75%, 1 MB
...76%, 1 MB
...76%, 1 MB
...76%, 1 MB
...77%, 1 MB
...77%, 1 MB
...77%, 1 MB
...78%, 1 MB
...78%, 1 MB
...79%, 1 MB
...79%, 1 MB
...79%, 1 MB
...80%, 1 MB
...80%, 1 MB
...81%, 1 MB
...81%, 1 MB
...81%, 1 MB
...82%, 1 MB
...82%, 1 MB
...82%, 1 MB
...83%, 1 MB
...83%, 1 MB
...84%, 1 MB
...84%, 1 MB
...84%, 1 MB
...85%, 1 MB
...85%, 1 MB
...85%, 1 MB
...86%, 1 MB
...86%, 1 MB
...87%, 1 MB
...87%, 1 MB
...87%, 1 MB
...88%, 1 MB
...88%, 1 MB
...89%, 1 MB
...89%, 1 MB
...89%, 1 MB
...90%, 1 MB
...90%, 1 MB
...90%, 1 MB
...91%, 1 MB
...91%, 1 MB
...92%, 1 MB
...92%, 1 MB
...92%, 1 MB
...93%, 1 MB
...93%, 1 MB
...93%, 1 MB
...94%, 1 MB
...94%, 1 MB
...95%, 1 MB
...95%, 1 MB
...95%, 1 MB
...96%, 1 MB
...96%, 1 MB
...97%, 1 MB
...97%, 2 MB
...97%, 2 MB
...98%, 2 MB
...98%, 2 MB
...98%, 2 MB
...99%, 2 MB
...99%, 2 MB

...100%, 2 MB     0    1    2    3    4    5    6    7    8    9  ...  930  931  932  933  934  935  936  937  938  Label
0  1.0  1.0  0.0  1.0  0.0  1.0  0.0  0.0  0.0  0.0  ...  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0    1.0
1  1.0  0.0  0.0  0.0  1.0  1.0  0.0  0.0  0.0  1.0  ...  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0    1.0
2  1.0  1.0  0.0  1.0  0.0  1.0  0.0  0.0  0.0  0.0  ...  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0    1.0
3  1.0  1.0  1.0  0.0  0.0  1.0  1.0  0.0  0.0  0.0  ...  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0    1.0
4  1.0  0.0  0.0  0.0  1.0  0.0  1.0  1.0  0.0  0.0  ...  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0  0.0    1.0

[5 rows x 940 columns]

Set up the training and testing sets

from sklearn.model_selection import train_test_split # noqa

X = df[df.columns.difference(["Label"])].values
y = df.loc[:, "Label"].values

Xtrain, Xtest, ytrain, ytest = \
    train_test_split(X, y, test_size=0.2, random_state=42)

Setup the models

# set up the group lasso GLM model
gl_glm = GLMCV(distr="binomial", tol=1e-3,
               group=group_idxs, score_metric="pseudo_R2",
               alpha=1.0, learning_rate=3, max_iter=100, cv=3, verbose=True)


# set up the lasso model
glm = GLMCV(distr="binomial", tol=1e-3,
            score_metric="pseudo_R2",
            alpha=1.0, learning_rate=3, max_iter=100, cv=3, verbose=True)

print("gl_glm: ", gl_glm)
print("glm: ", glm)

Out:

gl_glm:  <
Distribution | binomial
alpha | 1.00
max_iter | 100.00
lambda: 0.50 to 0.01
>
glm:  <
Distribution | binomial
alpha | 1.00
max_iter | 100.00
lambda: 0.50 to 0.01
>

Fit models

gl_glm.fit(Xtrain, ytrain)
glm.fit(Xtrain, ytrain)

Out:

/Users/mainak/Documents/github_repos/pyglmnet/pyglmnet/pyglmnet.py:864: UserWarning: Reached max number of iterations without convergence.
  "Reached max number of iterations without convergence.")

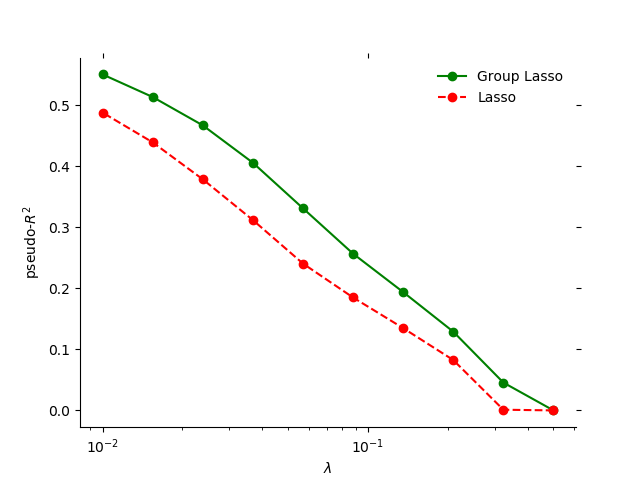
Visualize model scores on test set

plt.figure()
plt.semilogx(gl_glm.reg_lambda, gl_glm.scores_, 'go-')
plt.semilogx(glm.reg_lambda, glm.scores_, 'ro--')
plt.legend(['Group Lasso', 'Lasso'], frameon=False,
           loc='best')
plt.xlabel('$\lambda$')
plt.ylabel('pseudo-$R^2$')

plt.tick_params(axis='y', right='off')
plt.tick_params(axis='x', top='off')
ax = plt.gca()
ax.spines['top'].set_visible(False)
ax.spines['right'].set_visible(False)
plt.show()

Out:

/Users/mainak/Documents/github_repos/pyglmnet/examples/plot_group_lasso.py:89: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  plt.show()