Note
Click here to download the full example code
Tikhonov Regularization¶
Tikhonov regularization is a generalized form of L2-regularization. It allows us to articulate our prior knowlege about correlations between different predictors with a multivariate Gaussian prior. Here, we demonstrate how pyglmnet’s Tikhonov regularizer can be used to estimate spatiotemporal receptive fields (RFs) from neural data.
Neurons in many brain areas, including the frontal eye fields (FEF) have RFs, defined as regions in the visual field where visual stimuli are most likely to result in spiking activity.
These spatial RFs need not be static, they can vary in time in a systematic way. We want to characterize how such spatiotemporal RFs (STRFs) remap from one fixation to the next. Remapping is a phenomenon where the RF of a neuron shifts to process visual information from the subsequent fixation, prior to the onset of the saccade. The dynamics of this shift from the “current” to the “future” RF is an active area of research.
With Tikhonov regularization, we can specify a prior covariance matrix to articulate our belief that parameters encoding neighboring points in space and time are correlated.
The unpublished data are courtesy of Daniel Wood and Mark Segraves, Department of Neurobiology, Northwestern University.
# Author: Pavan Ramkumar <pavan.ramkumar@gmail.com>
# License: MIT
Imports
import os.path as op
import numpy as np
import pandas as pd
from pyglmnet import GLMCV
from spykes.ml.strf import STRF
import matplotlib.pyplot as plt
from tempfile import TemporaryDirectory
Download and fetch data files
from pyglmnet.datasets import fetch_tikhonov_data
with TemporaryDirectory(prefix="tmp_glm-tools") as temp_dir:
dpath = fetch_tikhonov_data(dpath=temp_dir)
fixations_df = pd.read_csv(op.join(dpath, 'fixations.csv'))
probes_df = pd.read_csv(op.join(dpath, 'probes.csv'))
probes_df = pd.read_csv(op.join(dpath, 'probes.csv'))
spikes_df = pd.read_csv(op.join(dpath, 'spiketimes.csv'))
spiketimes = np.squeeze(spikes_df.values)
Out:
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...2%, 0 MB
...2%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...4%, 0 MB
...4%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...7%, 0 MB
...7%, 0 MB
...8%, 0 MB
...8%, 0 MB
...8%, 0 MB
...9%, 0 MB
...9%, 0 MB
...10%, 0 MB
...10%, 0 MB
...10%, 0 MB
...11%, 0 MB
...11%, 0 MB
...12%, 0 MB
...12%, 0 MB
...12%, 0 MB
...13%, 0 MB
...13%, 0 MB
...13%, 0 MB
...14%, 0 MB
...14%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...16%, 0 MB
...16%, 0 MB
...17%, 0 MB
...17%, 0 MB
...17%, 0 MB
...18%, 0 MB
...18%, 0 MB
...18%, 0 MB
...19%, 0 MB
...19%, 0 MB
...20%, 0 MB
...20%, 0 MB
...20%, 0 MB
...21%, 0 MB
...21%, 0 MB
...22%, 0 MB
...22%, 0 MB
...22%, 0 MB
...23%, 0 MB
...23%, 0 MB
...24%, 0 MB
...24%, 0 MB
...24%, 0 MB
...25%, 0 MB
...25%, 0 MB
...25%, 0 MB
...26%, 0 MB
...26%, 0 MB
...27%, 0 MB
...27%, 0 MB
...27%, 0 MB
...28%, 0 MB
...28%, 0 MB
...29%, 0 MB
...29%, 0 MB
...29%, 0 MB
...30%, 0 MB
...30%, 0 MB
...30%, 0 MB
...31%, 0 MB
...31%, 0 MB
...32%, 0 MB
...32%, 0 MB
...32%, 0 MB
...33%, 0 MB
...33%, 0 MB
...34%, 0 MB
...34%, 0 MB
...34%, 0 MB
...35%, 0 MB
...35%, 0 MB
...36%, 0 MB
...36%, 0 MB
...36%, 0 MB
...37%, 0 MB
...37%, 0 MB
...37%, 0 MB
...38%, 0 MB
...38%, 0 MB
...39%, 0 MB
...39%, 0 MB
...39%, 0 MB
...40%, 0 MB
...40%, 0 MB
...41%, 0 MB
...41%, 0 MB
...41%, 0 MB
...42%, 0 MB
...42%, 0 MB
...42%, 0 MB
...43%, 0 MB
...43%, 0 MB
...44%, 0 MB
...44%, 0 MB
...44%, 0 MB
...45%, 0 MB
...45%, 0 MB
...46%, 0 MB
...46%, 0 MB
...46%, 0 MB
...47%, 0 MB
...47%, 0 MB
...48%, 0 MB
...48%, 0 MB
...48%, 0 MB
...49%, 0 MB
...49%, 1 MB
...49%, 1 MB
...50%, 1 MB
...50%, 1 MB
...51%, 1 MB
...51%, 1 MB
...51%, 1 MB
...52%, 1 MB
...52%, 1 MB
...53%, 1 MB
...53%, 1 MB
...53%, 1 MB
...54%, 1 MB
...54%, 1 MB
...54%, 1 MB
...55%, 1 MB
...55%, 1 MB
...56%, 1 MB
...56%, 1 MB
...56%, 1 MB
...57%, 1 MB
...57%, 1 MB
...58%, 1 MB
...58%, 1 MB
...58%, 1 MB
...59%, 1 MB
...59%, 1 MB
...60%, 1 MB
...60%, 1 MB
...60%, 1 MB
...61%, 1 MB
...61%, 1 MB
...61%, 1 MB
...62%, 1 MB
...62%, 1 MB
...63%, 1 MB
...63%, 1 MB
...63%, 1 MB
...64%, 1 MB
...64%, 1 MB
...65%, 1 MB
...65%, 1 MB
...65%, 1 MB
...66%, 1 MB
...66%, 1 MB
...66%, 1 MB
...67%, 1 MB
...67%, 1 MB
...68%, 1 MB
...68%, 1 MB
...68%, 1 MB
...69%, 1 MB
...69%, 1 MB
...70%, 1 MB
...70%, 1 MB
...70%, 1 MB
...71%, 1 MB
...71%, 1 MB
...72%, 1 MB
...72%, 1 MB
...72%, 1 MB
...73%, 1 MB
...73%, 1 MB
...73%, 1 MB
...74%, 1 MB
...74%, 1 MB
...75%, 1 MB
...75%, 1 MB
...75%, 1 MB
...76%, 1 MB
...76%, 1 MB
...77%, 1 MB
...77%, 1 MB
...77%, 1 MB
...78%, 1 MB
...78%, 1 MB
...79%, 1 MB
...79%, 1 MB
...79%, 1 MB
...80%, 1 MB
...80%, 1 MB
...80%, 1 MB
...81%, 1 MB
...81%, 1 MB
...82%, 1 MB
...82%, 1 MB
...82%, 1 MB
...83%, 1 MB
...83%, 1 MB
...84%, 1 MB
...84%, 1 MB
...84%, 1 MB
...85%, 1 MB
...85%, 1 MB
...85%, 1 MB
...86%, 1 MB
...86%, 1 MB
...87%, 1 MB
...87%, 1 MB
...87%, 1 MB
...88%, 1 MB
...88%, 1 MB
...89%, 1 MB
...89%, 1 MB
...89%, 1 MB
...90%, 1 MB
...90%, 1 MB
...91%, 1 MB
...91%, 1 MB
...91%, 1 MB
...92%, 1 MB
...92%, 1 MB
...92%, 1 MB
...93%, 1 MB
...93%, 1 MB
...94%, 1 MB
...94%, 1 MB
...94%, 1 MB
...95%, 1 MB
...95%, 1 MB
...96%, 1 MB
...96%, 1 MB
...96%, 1 MB
...97%, 1 MB
...97%, 1 MB
...97%, 1 MB
...98%, 1 MB
...98%, 1 MB
...99%, 2 MB
...99%, 2 MB
...99%, 2 MB
...100%, 2 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...8%, 0 MB
...8%, 0 MB
...8%, 0 MB
...8%, 0 MB
...8%, 0 MB
...8%, 0 MB
...8%, 0 MB
...9%, 0 MB
...9%, 0 MB
...9%, 0 MB
...9%, 0 MB
...9%, 0 MB
...9%, 0 MB
...9%, 0 MB
...9%, 0 MB
...10%, 0 MB
...10%, 0 MB
...10%, 0 MB
...10%, 0 MB
...10%, 0 MB
...10%, 0 MB
...10%, 0 MB
...11%, 0 MB
...11%, 0 MB
...11%, 0 MB
...11%, 0 MB
...11%, 0 MB
...11%, 0 MB
...11%, 0 MB
...11%, 0 MB
...12%, 0 MB
...12%, 0 MB
...12%, 0 MB
...12%, 0 MB
...12%, 0 MB
...12%, 0 MB
...12%, 0 MB
...13%, 0 MB
...13%, 0 MB
...13%, 0 MB
...13%, 0 MB
...13%, 0 MB
...13%, 0 MB
...13%, 0 MB
...13%, 0 MB
...14%, 0 MB
...14%, 0 MB
...14%, 0 MB
...14%, 0 MB
...14%, 0 MB
...14%, 0 MB
...14%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...15%, 0 MB
...16%, 0 MB
...16%, 0 MB
...16%, 0 MB
...16%, 0 MB
...16%, 0 MB
...16%, 0 MB
...16%, 0 MB
...17%, 1 MB
...17%, 1 MB
...17%, 1 MB
...17%, 1 MB
...17%, 1 MB
...17%, 1 MB
...17%, 1 MB
...17%, 1 MB
...18%, 1 MB
...18%, 1 MB
...18%, 1 MB
...18%, 1 MB
...18%, 1 MB
...18%, 1 MB
...18%, 1 MB
...19%, 1 MB
...19%, 1 MB
...19%, 1 MB
...19%, 1 MB
...19%, 1 MB
...19%, 1 MB
...19%, 1 MB
...19%, 1 MB
...20%, 1 MB
...20%, 1 MB
...20%, 1 MB
...20%, 1 MB
...20%, 1 MB
...20%, 1 MB
...20%, 1 MB
...21%, 1 MB
...21%, 1 MB
...21%, 1 MB
...21%, 1 MB
...21%, 1 MB
...21%, 1 MB
...21%, 1 MB
...21%, 1 MB
...22%, 1 MB
...22%, 1 MB
...22%, 1 MB
...22%, 1 MB
...22%, 1 MB
...22%, 1 MB
...22%, 1 MB
...23%, 1 MB
...23%, 1 MB
...23%, 1 MB
...23%, 1 MB
...23%, 1 MB
...23%, 1 MB
...23%, 1 MB
...23%, 1 MB
...24%, 1 MB
...24%, 1 MB
...24%, 1 MB
...24%, 1 MB
...24%, 1 MB
...24%, 1 MB
...24%, 1 MB
...25%, 1 MB
...25%, 1 MB
...25%, 1 MB
...25%, 1 MB
...25%, 1 MB
...25%, 1 MB
...25%, 1 MB
...25%, 1 MB
...26%, 1 MB
...26%, 1 MB
...26%, 1 MB
...26%, 1 MB
...26%, 1 MB
...26%, 1 MB
...26%, 1 MB
...27%, 1 MB
...27%, 1 MB
...27%, 1 MB
...27%, 1 MB
...27%, 1 MB
...27%, 1 MB
...27%, 1 MB
...27%, 1 MB
...28%, 1 MB
...28%, 1 MB
...28%, 1 MB
...28%, 1 MB
...28%, 1 MB
...28%, 1 MB
...28%, 1 MB
...29%, 1 MB
...29%, 1 MB
...29%, 1 MB
...29%, 1 MB
...29%, 1 MB
...29%, 1 MB
...29%, 1 MB
...29%, 1 MB
...30%, 1 MB
...30%, 1 MB
...30%, 1 MB
...30%, 1 MB
...30%, 1 MB
...30%, 1 MB
...30%, 1 MB
...31%, 1 MB
...31%, 1 MB
...31%, 1 MB
...31%, 1 MB
...31%, 1 MB
...31%, 1 MB
...31%, 1 MB
...31%, 1 MB
...32%, 1 MB
...32%, 1 MB
...32%, 1 MB
...32%, 1 MB
...32%, 1 MB
...32%, 1 MB
...32%, 1 MB
...33%, 1 MB
...33%, 1 MB
...33%, 1 MB
...33%, 1 MB
...33%, 1 MB
...33%, 1 MB
...33%, 1 MB
...33%, 1 MB
...34%, 2 MB
...34%, 2 MB
...34%, 2 MB
...34%, 2 MB
...34%, 2 MB
...34%, 2 MB
...34%, 2 MB
...35%, 2 MB
...35%, 2 MB
...35%, 2 MB
...35%, 2 MB
...35%, 2 MB
...35%, 2 MB
...35%, 2 MB
...35%, 2 MB
...36%, 2 MB
...36%, 2 MB
...36%, 2 MB
...36%, 2 MB
...36%, 2 MB
...36%, 2 MB
...36%, 2 MB
...36%, 2 MB
...37%, 2 MB
...37%, 2 MB
...37%, 2 MB
...37%, 2 MB
...37%, 2 MB
...37%, 2 MB
...37%, 2 MB
...38%, 2 MB
...38%, 2 MB
...38%, 2 MB
...38%, 2 MB
...38%, 2 MB
...38%, 2 MB
...38%, 2 MB
...38%, 2 MB
...39%, 2 MB
...39%, 2 MB
...39%, 2 MB
...39%, 2 MB
...39%, 2 MB
...39%, 2 MB
...39%, 2 MB
...40%, 2 MB
...40%, 2 MB
...40%, 2 MB
...40%, 2 MB
...40%, 2 MB
...40%, 2 MB
...40%, 2 MB
...40%, 2 MB
...41%, 2 MB
...41%, 2 MB
...41%, 2 MB
...41%, 2 MB
...41%, 2 MB
...41%, 2 MB
...41%, 2 MB
...42%, 2 MB
...42%, 2 MB
...42%, 2 MB
...42%, 2 MB
...42%, 2 MB
...42%, 2 MB
...42%, 2 MB
...42%, 2 MB
...43%, 2 MB
...43%, 2 MB
...43%, 2 MB
...43%, 2 MB
...43%, 2 MB
...43%, 2 MB
...43%, 2 MB
...44%, 2 MB
...44%, 2 MB
...44%, 2 MB
...44%, 2 MB
...44%, 2 MB
...44%, 2 MB
...44%, 2 MB
...44%, 2 MB
...45%, 2 MB
...45%, 2 MB
...45%, 2 MB
...45%, 2 MB
...45%, 2 MB
...45%, 2 MB
...45%, 2 MB
...46%, 2 MB
...46%, 2 MB
...46%, 2 MB
...46%, 2 MB
...46%, 2 MB
...46%, 2 MB
...46%, 2 MB
...46%, 2 MB
...47%, 2 MB
...47%, 2 MB
...47%, 2 MB
...47%, 2 MB
...47%, 2 MB
...47%, 2 MB
...47%, 2 MB
...48%, 2 MB
...48%, 2 MB
...48%, 2 MB
...48%, 2 MB
...48%, 2 MB
...48%, 2 MB
...48%, 2 MB
...48%, 2 MB
...49%, 2 MB
...49%, 2 MB
...49%, 2 MB
...49%, 2 MB
...49%, 2 MB
...49%, 2 MB
...49%, 2 MB
...50%, 2 MB
...50%, 2 MB
...50%, 2 MB
...50%, 2 MB
...50%, 2 MB
...50%, 2 MB
...50%, 2 MB
...50%, 2 MB
...51%, 3 MB
...51%, 3 MB
...51%, 3 MB
...51%, 3 MB
...51%, 3 MB
...51%, 3 MB
...51%, 3 MB
...52%, 3 MB
...52%, 3 MB
...52%, 3 MB
...52%, 3 MB
...52%, 3 MB
...52%, 3 MB
...52%, 3 MB
...52%, 3 MB
...53%, 3 MB
...53%, 3 MB
...53%, 3 MB
...53%, 3 MB
...53%, 3 MB
...53%, 3 MB
...53%, 3 MB
...54%, 3 MB
...54%, 3 MB
...54%, 3 MB
...54%, 3 MB
...54%, 3 MB
...54%, 3 MB
...54%, 3 MB
...54%, 3 MB
...55%, 3 MB
...55%, 3 MB
...55%, 3 MB
...55%, 3 MB
...55%, 3 MB
...55%, 3 MB
...55%, 3 MB
...56%, 3 MB
...56%, 3 MB
...56%, 3 MB
...56%, 3 MB
...56%, 3 MB
...56%, 3 MB
...56%, 3 MB
...56%, 3 MB
...57%, 3 MB
...57%, 3 MB
...57%, 3 MB
...57%, 3 MB
...57%, 3 MB
...57%, 3 MB
...57%, 3 MB
...58%, 3 MB
...58%, 3 MB
...58%, 3 MB
...58%, 3 MB
...58%, 3 MB
...58%, 3 MB
...58%, 3 MB
...58%, 3 MB
...59%, 3 MB
...59%, 3 MB
...59%, 3 MB
...59%, 3 MB
...59%, 3 MB
...59%, 3 MB
...59%, 3 MB
...60%, 3 MB
...60%, 3 MB
...60%, 3 MB
...60%, 3 MB
...60%, 3 MB
...60%, 3 MB
...60%, 3 MB
...60%, 3 MB
...61%, 3 MB
...61%, 3 MB
...61%, 3 MB
...61%, 3 MB
...61%, 3 MB
...61%, 3 MB
...61%, 3 MB
...62%, 3 MB
...62%, 3 MB
...62%, 3 MB
...62%, 3 MB
...62%, 3 MB
...62%, 3 MB
...62%, 3 MB
...62%, 3 MB
...63%, 3 MB
...63%, 3 MB
...63%, 3 MB
...63%, 3 MB
...63%, 3 MB
...63%, 3 MB
...63%, 3 MB
...64%, 3 MB
...64%, 3 MB
...64%, 3 MB
...64%, 3 MB
...64%, 3 MB
...64%, 3 MB
...64%, 3 MB
...64%, 3 MB
...65%, 3 MB
...65%, 3 MB
...65%, 3 MB
...65%, 3 MB
...65%, 3 MB
...65%, 3 MB
...65%, 3 MB
...66%, 3 MB
...66%, 3 MB
...66%, 3 MB
...66%, 3 MB
...66%, 3 MB
...66%, 3 MB
...66%, 3 MB
...66%, 3 MB
...67%, 3 MB
...67%, 3 MB
...67%, 3 MB
...67%, 3 MB
...67%, 3 MB
...67%, 3 MB
...67%, 3 MB
...68%, 3 MB
...68%, 4 MB
...68%, 4 MB
...68%, 4 MB
...68%, 4 MB
...68%, 4 MB
...68%, 4 MB
...68%, 4 MB
...69%, 4 MB
...69%, 4 MB
...69%, 4 MB
...69%, 4 MB
...69%, 4 MB
...69%, 4 MB
...69%, 4 MB
...70%, 4 MB
...70%, 4 MB
...70%, 4 MB
...70%, 4 MB
...70%, 4 MB
...70%, 4 MB
...70%, 4 MB
...70%, 4 MB
...71%, 4 MB
...71%, 4 MB
...71%, 4 MB
...71%, 4 MB
...71%, 4 MB
...71%, 4 MB
...71%, 4 MB
...72%, 4 MB
...72%, 4 MB
...72%, 4 MB
...72%, 4 MB
...72%, 4 MB
...72%, 4 MB
...72%, 4 MB
...72%, 4 MB
...73%, 4 MB
...73%, 4 MB
...73%, 4 MB
...73%, 4 MB
...73%, 4 MB
...73%, 4 MB
...73%, 4 MB
...73%, 4 MB
...74%, 4 MB
...74%, 4 MB
...74%, 4 MB
...74%, 4 MB
...74%, 4 MB
...74%, 4 MB
...74%, 4 MB
...75%, 4 MB
...75%, 4 MB
...75%, 4 MB
...75%, 4 MB
...75%, 4 MB
...75%, 4 MB
...75%, 4 MB
...75%, 4 MB
...76%, 4 MB
...76%, 4 MB
...76%, 4 MB
...76%, 4 MB
...76%, 4 MB
...76%, 4 MB
...76%, 4 MB
...77%, 4 MB
...77%, 4 MB
...77%, 4 MB
...77%, 4 MB
...77%, 4 MB
...77%, 4 MB
...77%, 4 MB
...77%, 4 MB
...78%, 4 MB
...78%, 4 MB
...78%, 4 MB
...78%, 4 MB
...78%, 4 MB
...78%, 4 MB
...78%, 4 MB
...79%, 4 MB
...79%, 4 MB
...79%, 4 MB
...79%, 4 MB
...79%, 4 MB
...79%, 4 MB
...79%, 4 MB
...79%, 4 MB
...80%, 4 MB
...80%, 4 MB
...80%, 4 MB
...80%, 4 MB
...80%, 4 MB
...80%, 4 MB
...80%, 4 MB
...81%, 4 MB
...81%, 4 MB
...81%, 4 MB
...81%, 4 MB
...81%, 4 MB
...81%, 4 MB
...81%, 4 MB
...81%, 4 MB
...82%, 4 MB
...82%, 4 MB
...82%, 4 MB
...82%, 4 MB
...82%, 4 MB
...82%, 4 MB
...82%, 4 MB
...83%, 4 MB
...83%, 4 MB
...83%, 4 MB
...83%, 4 MB
...83%, 4 MB
...83%, 4 MB
...83%, 4 MB
...83%, 4 MB
...84%, 4 MB
...84%, 4 MB
...84%, 4 MB
...84%, 4 MB
...84%, 4 MB
...84%, 4 MB
...84%, 4 MB
...85%, 4 MB
...85%, 5 MB
...85%, 5 MB
...85%, 5 MB
...85%, 5 MB
...85%, 5 MB
...85%, 5 MB
...85%, 5 MB
...86%, 5 MB
...86%, 5 MB
...86%, 5 MB
...86%, 5 MB
...86%, 5 MB
...86%, 5 MB
...86%, 5 MB
...87%, 5 MB
...87%, 5 MB
...87%, 5 MB
...87%, 5 MB
...87%, 5 MB
...87%, 5 MB
...87%, 5 MB
...87%, 5 MB
...88%, 5 MB
...88%, 5 MB
...88%, 5 MB
...88%, 5 MB
...88%, 5 MB
...88%, 5 MB
...88%, 5 MB
...89%, 5 MB
...89%, 5 MB
...89%, 5 MB
...89%, 5 MB
...89%, 5 MB
...89%, 5 MB
...89%, 5 MB
...89%, 5 MB
...90%, 5 MB
...90%, 5 MB
...90%, 5 MB
...90%, 5 MB
...90%, 5 MB
...90%, 5 MB
...90%, 5 MB
...91%, 5 MB
...91%, 5 MB
...91%, 5 MB
...91%, 5 MB
...91%, 5 MB
...91%, 5 MB
...91%, 5 MB
...91%, 5 MB
...92%, 5 MB
...92%, 5 MB
...92%, 5 MB
...92%, 5 MB
...92%, 5 MB
...92%, 5 MB
...92%, 5 MB
...93%, 5 MB
...93%, 5 MB
...93%, 5 MB
...93%, 5 MB
...93%, 5 MB
...93%, 5 MB
...93%, 5 MB
...93%, 5 MB
...94%, 5 MB
...94%, 5 MB
...94%, 5 MB
...94%, 5 MB
...94%, 5 MB
...94%, 5 MB
...94%, 5 MB
...95%, 5 MB
...95%, 5 MB
...95%, 5 MB
...95%, 5 MB
...95%, 5 MB
...95%, 5 MB
...95%, 5 MB
...95%, 5 MB
...96%, 5 MB
...96%, 5 MB
...96%, 5 MB
...96%, 5 MB
...96%, 5 MB
...96%, 5 MB
...96%, 5 MB
...97%, 5 MB
...97%, 5 MB
...97%, 5 MB
...97%, 5 MB
...97%, 5 MB
...97%, 5 MB
...97%, 5 MB
...97%, 5 MB
...98%, 5 MB
...98%, 5 MB
...98%, 5 MB
...98%, 5 MB
...98%, 5 MB
...98%, 5 MB
...98%, 5 MB
...99%, 5 MB
...99%, 5 MB
...99%, 5 MB
...99%, 5 MB
...99%, 5 MB
...99%, 5 MB
...99%, 5 MB
...99%, 5 MB
...100%, 5 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...0%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...1%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...2%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...3%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...4%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...5%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...6%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 0 MB
...7%, 1 MB
...7%, 1 MB
...7%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...8%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...9%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...10%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...11%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...12%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...13%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...14%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 1 MB
...15%, 2 MB
...15%, 2 MB
...15%, 2 MB
...15%, 2 MB
...15%, 2 MB
...15%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...16%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...17%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...18%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...19%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...20%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...21%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...22%, 2 MB
...23%, 2 MB
...23%, 2 MB
...23%, 2 MB
...23%, 2 MB
...23%, 2 MB
...23%, 2 MB
...23%, 2 MB
...23%, 3 MB
...23%, 3 MB
...23%, 3 MB
...23%, 3 MB
...23%, 3 MB
...23%, 3 MB
...23%, 3 MB
...23%, 3 MB
...23%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...24%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...25%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...26%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...27%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...28%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...29%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...30%, 3 MB
...31%, 3 MB
...31%, 3 MB
...31%, 3 MB
...31%, 3 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...31%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...32%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...33%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...34%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...35%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...36%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...37%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...38%, 4 MB
...39%, 4 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...39%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...40%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...41%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...42%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...43%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...44%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...45%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 5 MB
...46%, 6 MB
...46%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...47%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...48%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...49%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...50%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...51%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...52%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...53%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 6 MB
...54%, 7 MB
...54%, 7 MB
...54%, 7 MB
...54%, 7 MB
...54%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...55%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...56%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...57%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...58%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...59%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...60%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...61%, 7 MB
...62%, 7 MB
...62%, 7 MB
...62%, 7 MB
...62%, 7 MB
...62%, 7 MB
...62%, 7 MB
...62%, 7 MB
...62%, 7 MB
...62%, 8 MB
...62%, 8 MB
...62%, 8 MB
...62%, 8 MB
...62%, 8 MB
...62%, 8 MB
...62%, 8 MB
...62%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...63%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...64%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...65%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...66%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...67%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...68%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...69%, 8 MB
...70%, 8 MB
...70%, 8 MB
...70%, 8 MB
...70%, 8 MB
...70%, 8 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...70%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...71%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...72%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...73%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...74%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...75%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...76%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...77%, 9 MB
...78%, 9 MB
...78%, 9 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...78%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...79%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...80%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...81%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...82%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...83%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...84%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 10 MB
...85%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...86%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...87%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...88%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...89%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...90%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...91%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...92%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 11 MB
...93%, 12 MB
...93%, 12 MB
...93%, 12 MB
...93%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...94%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...95%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...96%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...97%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...98%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...99%, 12 MB
...100%, 12 MB
Design spatial basis functions
n_spatial_basis = 36
n_temporal_basis = 7
strf_model = STRF(patch_size=50, sigma=5,
n_spatial_basis=n_spatial_basis,
n_temporal_basis=n_temporal_basis)
spatial_basis = strf_model.make_gaussian_basis()
strf_model.visualize_gaussian_basis(spatial_basis)

Out:
/Users/mainak/anaconda3/lib/python3.7/site-packages/spykes/ml/strf.py:110: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
plt.show()
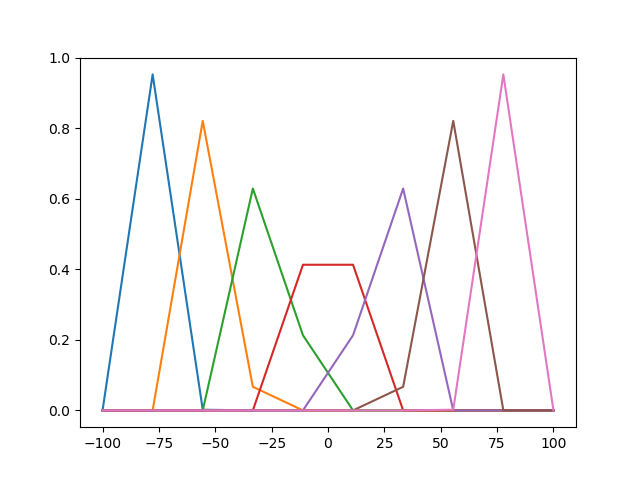
Design temporal basis functions
time_points = np.linspace(-100., 100., 10.)
centers = [-75., -50., -25., 0, 25., 50., 75.]
temporal_basis = strf_model.make_raised_cosine_temporal_basis(
time_points=time_points,
centers=centers,
widths=10. * np.ones(7))
plt.plot(time_points, temporal_basis)
plt.show()
Out:
/Users/mainak/Documents/github_repos/pyglmnet/examples/plot_tikhonov.py:78: DeprecationWarning: object of type <class 'float'> cannot be safely interpreted as an integer.
time_points = np.linspace(-100., 100., 10.)
/Users/mainak/Documents/github_repos/pyglmnet/examples/plot_tikhonov.py:85: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
plt.show()
Design parameters
# Spatial extent
n_shape = 50
n_features = n_spatial_basis
# Window of interest
window = [-100, 100]
# Bin size
binsize = 20
# Zero pad bins
n_zero_bins = int(np.floor((window[1] - window[0]) / binsize / 2))
Build design matrix
bin_template = np.arange(window[0], window[1] + binsize, binsize)
n_bins = len(bin_template) - 1
probetimes = probes_df['t_probe'].values
spatial_features = np.zeros((0, n_features))
spike_counts = np.zeros((0,))
fixation_id = np.zeros((0,))
# For each fixation
for fx in fixations_df.index[:1000]:
# Fixation time
fixation_time = fixations_df.loc[fx]['t_fix_f']
this_fixation_spatial_features = np.zeros((n_bins, n_spatial_basis))
this_fixation_spikecounts = np.zeros(n_bins)
unique_fixation_id = fixations_df.loc[fx]['trialNum_f']
unique_fixation_id += 0.01 * fixations_df.loc[fx]['fixNum_f']
this_fixation_id = unique_fixation_id * np.ones(n_bins)
# Look for probes in window of interest relative to fixation
probe_ids = np.searchsorted(probetimes,
[fixation_time + window[0] + 0.1,
fixation_time + window[1] - 0.1])
# For each such probe
for probe_id in range(probe_ids[0], probe_ids[1]):
# Check if probe lies within spatial region of interest
fix_row = fixations_df.loc[fx]['y_curFix_f']
fix_col = fixations_df.loc[fx]['x_curFix_f']
probe_row = probes_df.loc[probe_id]['y_probe']
probe_col = probes_df.loc[probe_id]['x_probe']
if ((probe_row - fix_row) > -n_shape / 2 and
(probe_row - fix_row) < n_shape / 2 and
(probe_col - fix_col) > -n_shape / 2 and
(probe_col - fix_col) < n_shape / 2):
# Get probe timestamp relative to fixation
probe_time = probes_df.loc[probe_id]['t_probe']
probe_bin = np.where(bin_template < (probe_time - fixation_time))
probe_bin = probe_bin[0][-1]
# Define an image based on the relative locations
img = np.zeros(shape=(n_shape, n_shape))
row = int(-np.round(probe_row - fix_row) + n_shape / 2 - 1)
col = int(np.round(probe_col - fix_col) + n_shape / 2 - 1)
img[row, col] = 1
# Compute projection
basis_projection = strf_model.project_to_spatial_basis(
img, spatial_basis)
this_fixation_spatial_features[probe_bin, :] = basis_projection
# Count spikes in window of interest relative to fixation
bins = fixation_time + bin_template
searchsorted_idx = np.searchsorted(spiketimes,
[fixation_time + window[0],
fixation_time + window[1]])
this_fixation_spike_counts = np.histogram(
spiketimes[searchsorted_idx[0]:searchsorted_idx[1]], bins)[0]
# Accumulate
fixation_id = np.concatenate((fixation_id, this_fixation_id), axis=0)
spatial_features = np.concatenate((spatial_features,
this_fixation_spatial_features), axis=0)
spike_counts = np.concatenate((spike_counts,
this_fixation_spike_counts), axis=0)
# Zero pad
spatial_features = np.concatenate((
spatial_features, np.zeros((n_zero_bins, n_spatial_basis))))
fixation_id = np.concatenate((fixation_id, -999. * np.ones(n_zero_bins)))
# Convolve with temporal basis
features = strf_model.convolve_with_temporal_basis(spatial_features,
temporal_basis)
# Remove zeropad
features = features[fixation_id != -999.]
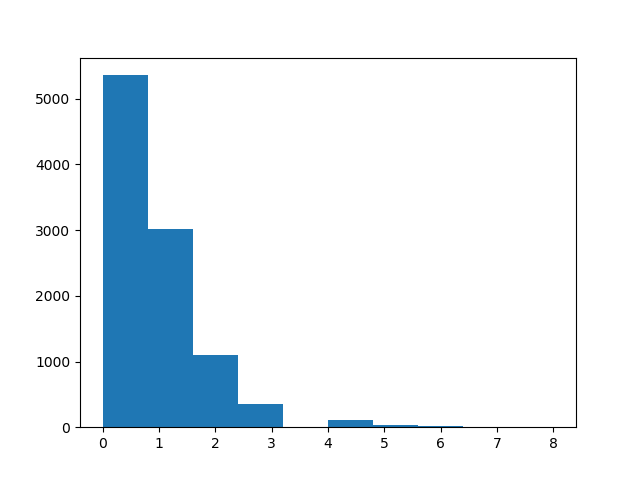
Visualize the distribution of spike counts
plt.hist(spike_counts, 10)
plt.show()
Out:
/Users/mainak/Documents/github_repos/pyglmnet/examples/plot_tikhonov.py:192: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
plt.show()
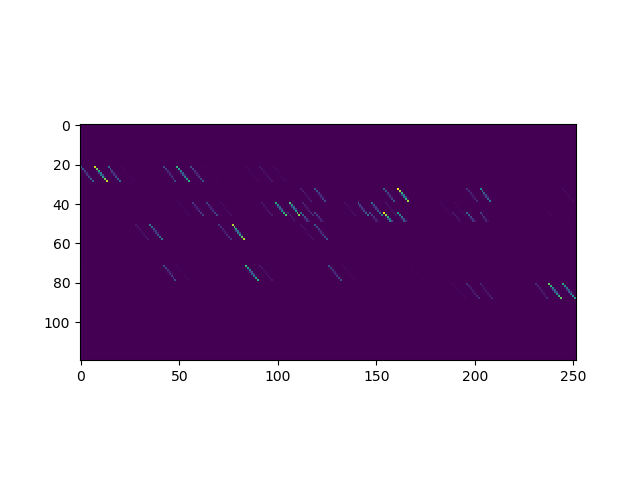
Plot a few rows of the design matrix
plt.imshow(features[30:150, :], interpolation='none')
plt.show()
Out:
/Users/mainak/Documents/github_repos/pyglmnet/examples/plot_tikhonov.py:198: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
plt.show()
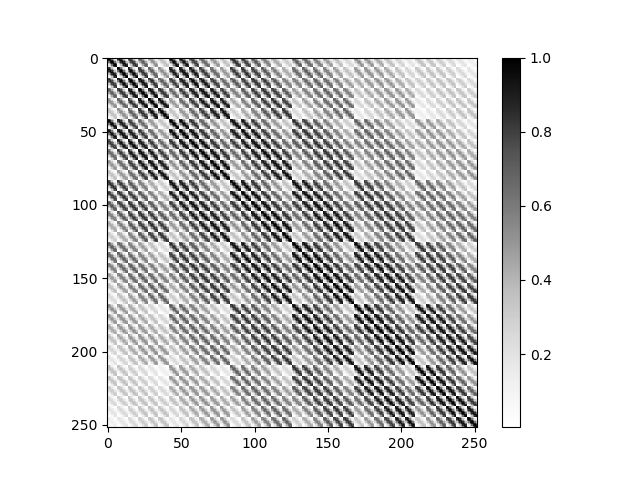
Design prior covariance matrix for Tikhonov regularization
prior_cov = strf_model.design_prior_covariance(
sigma_temporal=3.,
sigma_spatial=5.)
plt.imshow(prior_cov, cmap='Greys', interpolation='none')
plt.colorbar()
plt.show()
np.shape(prior_cov)
Out:
/Users/mainak/Documents/github_repos/pyglmnet/examples/plot_tikhonov.py:208: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
plt.show()
Fit models
from sklearn.model_selection import train_test_split # noqa
Xtrain, Xtest, Ytrain, Ytest = train_test_split(
features, spike_counts,
test_size=0.2,
random_state=42)
from pyglmnet import utils # noqa
n_samples = Xtrain.shape[0]
Tau = utils.tikhonov_from_prior(prior_cov, n_samples)
glm = GLMCV(distr='poisson', alpha=0., Tau=Tau, score_metric='pseudo_R2', cv=3)
glm.fit(Xtrain, Ytrain)
print("train score: %f" % glm.score(Xtrain, Ytrain))
print("test score: %f" % glm.score(Xtest, Ytest))
weights = glm.beta_
Out:
/Users/mainak/Documents/github_repos/pyglmnet/pyglmnet/pyglmnet.py:864: UserWarning: Reached max number of iterations without convergence.
"Reached max number of iterations without convergence.")
train score: 0.048506
test score: 0.015134
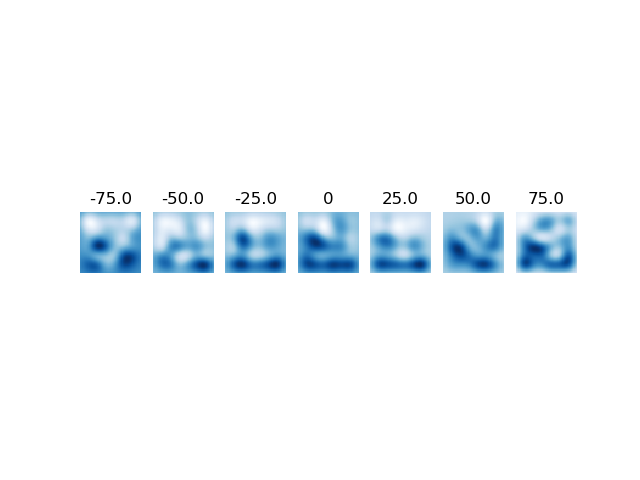
Visualize
for time_bin_ in range(n_temporal_basis):
RF = strf_model.make_image_from_spatial_basis(
spatial_basis,
weights[range(time_bin_, n_spatial_basis * n_temporal_basis,
n_temporal_basis)])
plt.subplot(1, n_temporal_basis, time_bin_ + 1)
plt.imshow(RF, cmap='Blues', interpolation='none')
titletext = str(centers[time_bin_])
plt.title(titletext)
plt.axis('off')
plt.show()
Out:
/Users/mainak/Documents/github_repos/pyglmnet/examples/plot_tikhonov.py:246: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
plt.show()
Total running time of the script: ( 6 minutes 12.349 seconds)